Computational Theory of Mind

Introduction: Characterising Semantic Content

The fundamental semantic unit on Brandom’s picture of semantics is that of the vocabulary. Opposed to traditional accounts of semantics which seek to analyse of the meaning of statements by breaking-down the semantic structures into discrete semantic units, Brandom allows (in his Between Saying and Doing) that vocabularies exist as self-sustaining structures, that do not admit such absolute decomposition. In support of the view he points to the failure of the logicist program in the philosophy of mathematics, where the robust vocabulary of mathematics cannot be semantically equated with statements expressible in purely logical vocabulary.

He further defends the general claim that the traditional project of semantic analysis is misguided by Sellarsian arguments against the myth of the given. Any candidate analysis will involve a decomposition of the whole structure into some primitive semantic units in the base vocabulary. The traditional empiricist program would seek to analyse all semantic understanding in terms of understanding primitive observational reports. So assuming that some form of empiricism is true, then some base observational reports are semantically autonomous of the broader vocabulary. The broader vocabulary depends for its semantic cogency on the empiricist’s autonomous base, in terms of which the it is to be analysed. However, for any candidate base vocabulary we can argue that we cannot be deemed to understand the semantic primitives unless we know how they are to be practically deployed within the network of our broader vocabulary. For example, assume the empiricist wants a reduction of our knowledge into a base phenomenalist observational vocabulary. How can we be considered to understand the claim that: $x \text{ is red}$ if we do not accept that this commits us (by inferential connection) to the claim that $x \text{ is not blue}?$ We cannot. The argument generalises for any reductive programme of semantic analysis, since semantic understanding is to be demonstrated by practical fluency with the semantic primitives in question and fluency is a holistic notion relative to the broader vocabulary. Hence the proper study of semantics is not exhausted by the process of analysis; crucially we can see that semantic content of our primitive terms (i.e. what we understand when we understand the meanings of terms) is at least in part conferred upon them by their role in a wider inferentially mediated setting.

On this understanding the meaning of any syntactic constructions are to be understood relative to the knowledge of a broader vocabulary, and we demonstrate the understanding of a vocabulary by our ability to enter into certain kinds of practices. In mathematics, for instance, we can be said to know the meaning of the term “proof” only when we inferentially trace the path from our assumptions to the statement we set out to prove and subsequently react appropriately to the statement of a proof completion $\dashv.$ It would be a semantic error to continuing drawing deductions after articulating a valid proof. This kind of practical ability which we expect of any users of our vocabulary has the effect of delimiting the conditions under which a term is being meaningfully used. In this manner Brandom argues that pragmatics contributes to the semantics of our vocabulary.

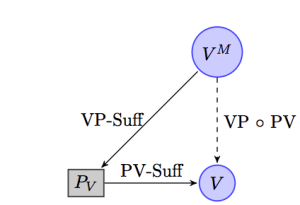
He further notes that where we have access to meta-vocabulary $V^{M}$ which describes exactly how demonstrating facility with a set of practices $P_{V}$ is sufficient to demonstrate a semantic understanding of the vocabulary $V$ , the meta-vocabulary will be able to express why such practices are apt to constrain the meaning of our vocabulary. He depicts the relationship as follows:

The thought is that for any particular vocabulary $V$ there is a set of practices which when enacted are deemed $PV$ -sufficient to indicate mastery of the vocabulary, such that any meta-language $V^{M}$ will be able to describe (specify) those actions which indicate competence. A fully expressive meta language results from a kind of composition function which recognises the conditions of practical competence as a sufficient condition for determining semantic content of $V$ and articulates the rules for deployment of a $VP$ -sufficient description to perfectly specify those practices pertinent for the evaluation of competency with vocabulary for $V$ . These for Brandom are the basic meaning-use relations, and for each particular vocabulary-in-use there is a process by which we can recursively generate the appropriate meta-language. To do so we will show below how each mapping between practices and vocabularies is taken to preserve analogous categorical structures which can be recovered (one from another) by a chain of equivalence proofs, at each stage.

Intuitive Sellarsian Examples

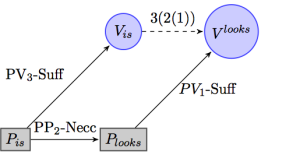
To illustrate the types of considerations this set up allows, we examine another Sellarsian argument. Namely, the claim that the “looks- $\phi$ ” vocabulary presupposes (i.e. must be able to express) the “is- $\phi$ ” vocabulary in so far as the pragmatic ability to discern appearance from actuality assumes the ability to identify the actual.

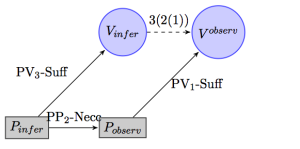
Again we denote the composition relation by the dashed arrow, but the point is clear, since the expression of perceptual modalities requires the ability to practically distinguish objects by sight accurately. It is a necessary condition of such an ability that we are able to identify things in their actual condition, which is a ability sufficient to confer meaning on existential and identity claims. Hence, talk of appearance amounts to the withholding of the existential claim, and only by composing our abilities can we generate a suitably expressive language to capture the perceptual modalities. Similarly, the argument we sketched above, that there is no autonomous observational vocabulary from which we build our semantics relies on the idea that observational expression assumes a practical capacity that in turn presupposes the inferential capacity (which is at least sufficient) for an appropriately broad semantic understanding, contrary to the supposed semantic autonomy of observational reports. Only by composing the two abilities can we determine a language sufficient to articulate the conditions under which observational reports are meaningful.

Recall that the semantic understanding of the claim “x is red” requires the ability to not equate the object x with any blue object. In particular we must be able to wield an inferential capacity which gives the lie to the idea that we understand color observations independently of anything else.

Santa-Speak and Speaking about Santa-Speak

Now for a brief digression.

Santa laughs and he laughs heartily. We can build a machine which describes how Santa laughs, and it can be used to establish whether any program generating a laughter track appropriately simulates Santa’s laugh. The following example over and above the previous cases is of central significance, not just for its relative clarity but also because of how the setting has a connection to computational linguistics. The basic idea is that we take a set $\{ a, h, ... \}$ of syntactic primitives and allow various composition operations or rules as described by a machine. In particular, consider the specification of a non-deterministic finite state automata which articulates (prints) how Santa laughs. There is an initial state and two intermediary states. The fourth state is an end state so there are no actions specified.

The rules are such that for any legitimate string of inputs Santa always laughs a string $(h, ...!)$ , with a random variation, of $(ha) \text{ or } (ho)$ being produced at state two. After which he might begin to chuckle anew, or end with a hearty exclamation. For any finite string of inputs the purpose of the machine is to determine whether it is a legitimate string. It will reject any string as illegitimate if it yields a premature halt.

Relating Automata to Meaning Use Diagrams

The notion of producing a legitimate string is analogous to the notion of competent linguistic practice. In effect the rules of syntactic construction put forward in the state-table are a normative constraint on how deploy Santa’s alphabet $\{a, h, o, ! \}$ in the way it is “meaningful” for Santa. The following diagram gives the right structure:

The ”meta-language” of the state-table (above) describes the practices appropriate for the proper syntactic representation of Santa’s laugh. The point is that if we can describe this kind of practical performance constraint we can specify the pre-conditions and post-conditions appropriate to render certain utterances “meaningful” or at least syntactically correct. One fine example of this trend is the manner in which recursive languages can be specified in a category free language, which in turn is demonstrably understood by an ability to deploy the differential response patterns of an appropriate push-down automata. Again the picture is as follows:

We shall now sketch the details that show this relation to describe a valid theorem.

Context Free Grammars

First recall that a context free grammar is a phase structure grammar $G = (N, T, P, S)$ where $N$ is the set of a non-terminal (complex) symbols, $T$ is the set of terminal (atomic) symbols, $P$ is the set of production rules and $S$ is the start symbol a member of $N$ . For our phase structure grammar to be a context free grammar, we need to further specify that if $x \rightarrow y$ is a production rule for G, then $x \in N, y \in (N \cup T)^{*}$ . This is just to say that any non-terminal string can be transformed into any constructable string whatsoever, even the empty string. The language generated by $G$ is denoted:

$L(G) = \{ x | x \in T^{*} \text{ and } S \Rightarrow^{*} x \}$

where $\Rightarrow^{*}$ defines the “derivation” relation we have in the language by applications of the production rules in $i$ steps where $i \geq 0.$ So the language is composed of a set of strings generated by manipulations of the start string; the legitimate manipulations are determined by a set of production rules. For example if we specify the production rules of $G$ as follows: $\text{ (1) } S \rightarrow AA, \text{ (2) } A \rightarrow AAA|bA|Ab|a$ , then our grammar is category free, and any language generated will be a category free language. If you’re familiar with basic logical languages you can think of the production rules as decomposition operations in a tableau proof e.g. $(\phi \wedge \psi)\vee (\tau \wedge \psi)$ is produced from, or decomposes to $(\phi \wedge \psi)$ or $(\tau \wedge \psi)$ . The production rule might be $C \rightarrow AB$

This point should illustrate how adherence to (and recognition of) these production rules is taken to be sufficient for an understanding of the language; more radically, Brandom wants to say that the practice of these rules confers legitimacy on strings created in the language. Like the Santa example above, we can create a machine to test whether any string is “grammatical” i.e. legitimate, on the basis of the definition of $G$ .

You, me and Pushdown Automata

So who understands these languages? Or better said, what behaviour is indicative of this understanding, and who enacts it? Pushdown automata are machines with a virtual memory, like the Santa-speak finite state machine, but augmented with a memory stack.

Definition: Pushdown automata: are sextuples ( $Q, \Pi, \Gamma, \delta, q_{0}, F$ ) where $Q$ is the set of finite machine states, $\Pi$ is the input alphabet and $\Gamma$ is the stack alphabet representative of the machine’s memory. We let $q_{0}$ be the initial machine states and $F \subseteq Q$ is the set of final states or terminal nodes. The crucial feature of each machine is the transition function $\delta: Q \times (\Pi \cup \{\epsilon\}) \times (\Gamma \cup \{\epsilon\}) \mapsto Q \times (\Gamma \cup \{\epsilon\})$

The thought is that a machine takes inputs of an ordered triple in the form the active machine state, memory and a given string read from left to right $< [ x ], y, z, w ... >$ , and then operates according to the specifications of the transition function which induces a new machine state and an updated memory, receptive for the novel string instructions $< [y], z, w ... >$ . After each transition an element of the input string is popped out of the memory stack, and a novel element pushed into the stack. This definition leaves it an open question as to whether the transition function is ultimately deterministic or non-deterministic.

So now the idea is to show that for every context free grammar $G$ there is a pushdown automata which operates to test for accordance to the parse/production rules essential to $G$ . In this manner any string input can be tested by the PDA to determine whether the string is a legitimate element of $L(G)$ . The manner in which we show this is possible is to first define the language for a machine $M$ as the set of strings $L(M)$ accepted by $M$ , and then show that this set of strings is the same as the set of strings legitimately produced by derivations in $G.$ An accepted string is defined as one which when input into the PDA ensures that the machine comes to a halt (final state) with an empty memory stack i.e. that the string is entirely parsed string. It has exhausted its “problem string”. To facilitate the proof consider the following lemma.

Lemma The Greibach Normal Form of a context free grammar $G$ is such that all the rules of production have one of the following forms:

$A \rightarrow aA_{1}A_{2} ...A_{n}$
$A \rightarrow a$
$S \rightarrow \epsilon$

where $a \in \Pi$ and $A_{i} \in N - \{S\} \text{ for } i = 1, 2, ... n.$

There is an algorithm for converting all context free grammars $G$ into an equivalent Greibach Normal Form grammars $G^{'}$ . Consider a schematic example of how we can change the rules of a grammar without impacting the language generated by that grammar. Suppose that we have a production rule of the form $A \rightarrow uBz \in P$ , then we can remove this rule and replace it with $A \rightarrow uw_{1}z | uw_{2}z| .... |uw_{n}z \in P^{'}$ , where $B \rightarrow w_{1} | w_{2} | .... |w_{n}$ were the productions rules for $B \in P.$ It is then straightforward to show that any $\Rightarrow^{*}$ derivation made with the rules $P$ can be established by using the rules $P^{'}.$ In this fashion we replace the rules of the grammar $G$ to establish the grammar $G^{'}$ in Griebach normal form. The proof of the existence of the algorithm for the general case is done by induction, but the details aren’t terribly instructive. The point is that we can put any set of production rules into a form that aids parsing. If you’re inclined to think that something similar is involved in human cognition you can think of this as an efficiency measure to aid our focus on the particulars, where for every complex utterance we first isolate the “subject” of the statement and subsequently process the relations.

Theorem: For every CFG which generates $L(G)$ , there is a PDA such that $L(G) = L(M)$

Proof Let $G = (N, T, P, S)$ be a context free grammar in Griebach normal form that generates $L$ . An extended PDA $M$ with start state $q_{0}$ is defined by:

$Q_{M} = \{q_{0}, q_{1} \}$
$\Pi_{M} = T$
$\Gamma_{M}$ $= N - \{S\}$
$F_{M} = \{q_{1} \}$

and we define the transition function as follows:

(1) $\delta(q_{0}, a, \epsilon) = \{[q_{1}, w ] \text{ : } S \rightarrow aw \in P \}$

(2) $\delta(q_{1}, a, A) = \{ [q_{1}, w] \text{ : } A \rightarrow aw \in P \text{ and } A \in N - \{S\} \}$

(3) $\delta(q_{0}, \epsilon, \epsilon) = \{ [q_{1}, \epsilon] \} \text{ if } S \rightarrow \epsilon \in P$

These are sufficient because of the insistence on the Greibach normal form. The $\delta$ function ensures that each transition updates the memory stack of the push-down automata so that the PDA will cycle through the non-terminal variables $A_{1}... A_{n}$ until it halts, so long as there is an input string in accordance with the grammar of $G$ . The transition function is undefined otherwise i.e. it would fail to process ungrammatical strings. We shall now show that for any computation $[q_{0}, u, \epsilon] \vdash [q_{1} \epsilon, w]$ , there is a derivation $S \Rightarrow^{*} uw$ with $u \in \Pi_{M}^{+}$ and $w \in N^{*}$

Our base case is the one step computation, and an application of the rule of the form $S \rightarrow aw$ ensures that this case holds.

IH For all $n-1$ -step computations of strings $uw$ we can find a derivation $S \Rightarrow_{n-1} uw$ such that $uw \in L(G)$

Now for the $n-th$ step, we take a computation $[q_{0}, u, \epsilon ] \vdash^{n} [q_{1}, \epsilon, w]$ with $u = va \in \Pi$ and $w = w_{1}w_{2} \in N^{+}$ , which can be rewritten:

$[q_{0}, va, \epsilon] \vdash^{n-1} [q_{1}, a, Aw_{2}] \vdash [q_{1}, \epsilon, w_{1}w_{2}]$

By the inductive hypothesis and the Greibach production rules we have it that there is an $\Rightarrow^{n}$ derivation such that: $S \Rightarrow^{n-1} vAw_{2} \Rightarrow vaw_{1}w_{2} = uw$ . The case where the computation proceeds from the initial state by the application of the third transition rule, is handled similarly. Hence any positive length string $u$ is derivable in $G$ if there is a computation that processes $u$ without prematurely halting.

This shows that $L(M) \subseteq L(G)$ , the other direction is analogous and proven by Sudkamp. This completes the proof. $\dashv$

To see that the language $L(M)$ is recursively enumerable we need only observe that for any PDA we can describe a two-stack Turing machine that is equivalent to it. This theorem can also be found in Sudkamp’s Languages and Machines. As such, any CFG dictates a PDA and all PDAs generate recursively constructible languages. It is in this sense that context free grammars are said to be sufficient to specify the functions of recursive languages and so serve as a normative meta-language for describing the syntactic construction rules of a given recursively enumerable language. In this way Brandom argues for the categorical relations between patterns languages and patterns of performance.

Automata, Differential Response and Algorithmic Elaboration

So we know that functional capacity with the procedures enacted by a PDA is sufficient to generate a veneer of competence with a recursive language. If all of this is beginning to sound like an agonisingly exact rendition of the Turing Test, rest assured that Brandom has something more in mind. Linguistic competence is only one criteria is any test for sapience. He writes:

The issue is whether whatever capacities constitute sapience, whatever practices or abilities it involves, admit of such a substantive practical algorithmic decomposition. If we think of sapience as consisting in the capacity to deploy a vocabulary, so as being what the Turing test is a test for, then since we are thinking of sapience as a kind of symbol use, the target practices-or-abilities will also involve symbols. But this is an entirely separate, in principal independent, commitment. That is why […] classical symbolic AI-functionalism is merely one species of the broader genus of algorithmic practical elaboration AI-functionalism, and the central issues are mislocated if we focus on the symbolic nature of thought rather than the substantive practical algorithmic analyzability of whatever practices-or-abilities are sufficient for sapience. (BSaDpg 77)

This is pregnant passage, but the key take away is that the conditions of sapience are unspecified, but taken to be specifiable by means of algorithmic action. Plausibly the conditions involve more than linguistic competence, but can nevertheless be described as certain kind of differential response to an array of stimuli a la Quine; where the input strings can be thought of as composed of as various information streams, and the transition functions are modeled on features of our cognitive processing. The view of AI-functionalism at the heart of this story is premised on the idea that certain algorithmically specifiable computer languages are apt to serve as pragmatic meta-vocabularies for our natural languages. As such, any pattern of differential response we care to mention can be specified algorithmically, if it can be discussed in natural language at all. Hence, whatever the future course of scientific discovery, so long as the conditions of sapience can be artificially implemented and described in natural language, we can develop an algorithmic elaboration of patterns of the differential response involved. So there is, in principal, no bar for the development of artificial intelligence, if we can come to understand what in fact makes us tick.

Before considering the wider ramifications of this view we shall examine (in the next post) a detailed example of an algorithmic elaboration of the abilities and practices deemed to be pragmatically sufficient to warrant ascriptions of linguistic competence. This will be paradigmatic for the broader stripe of “competency” claims Brandom needs to make if he is to isolate the conditions of sapience algorithmically.

Aspiring PI

"An orgy of abstract informality" – reader review

Tag Archives: Computational Theory of Mind

Brandom’s Sufficiency Claims