Tag Archives: Infinity

Coding into the Natural Numbers: The Very Idea

Posted in Logic, Semantics, Things that are true by

Have you ever been introduced to too many people at a party and come up with ad hoc nicknames, to keep track of who they were, how they knew the host etc? If so, congratulations you’ve successfully invented a coding schema.

Now imagine a party at Hilbert’s hotel with all its infinite guests. Suppose that each night they form a congo line alternating positions at random each night. It’s your task to keep track of the order of who follows who, but given that you can’t remember all their names you try to come up with a coding scheme which would uniquely identify each individual in the line… unfortunately the line is not finite, so you’ll need an infinite set of codes to describe the order of the line:

It’s at this point you might think of trying to number them. Only a moment later you realise how convenient this procedure is; after all an infinite of people can be labeled by an infinity of numerals! Call a congo line a sequence <a_{0}, a_{1} .... a_{n} > where each of the dancers a_{i} are currently nameless, and unknown to you.

We will consider a coding technique invented by Godel. The approach uses the fact that there are an infinity of primes to name the infinity of congo dancers. So for example we might specify the first dancer a_{1} = p_{1}^{a_{1}+1} using the fact of the uniqueness of prime factorization to ensure that this label is unique. The “+1” is crucial for ensuring that we always have a positive exponent. So using this technique to we could define a concatenation operation on a congo line as the product of their unique labels:  

<a_{1}*a_{2}, ... *a_{n} > = \Pi_{i \leq n} p_{i}^{a_{i}+1}

In this instance we characterize each line as the product of the labels of the dancers. We let the empty sequence

  • <> = 1
  • <a_{1}*a_{2}> = 2^{a_{1}+1} \cdot 3^{a_{2}+1}
  • <a_{1}*a_{2}*a_{3}> = 2^{a_{1}+1} \cdot 3^{a_{2}+1} \cdot 5^{a_{3}+1}
  • etc, etc…

But this doesn’t make much sense; how can we add or multiply dancers? Not obviously. However we could begin by categorizing types of dancers as graceful, quick, sultry, smooth, etc, then we can assign each type a distinct number, so the coding maps each type into a region of primes determined by the type of dancers in the sequence, thereby allowing us to represent each congo line as a chain of prime numbers with each member “scored” according to their type. Allow that we have a (in)finite alphabet of types, we say the types are coded as follow

  • #a_{i} := 2
  • #b_{i} := 3
  • #c_{i} : = 6
  • … associated with as many code numbers as required.

Now that we have named the parts, we might want to name the whole line. So we need to find a unique label for any sequence of dancers. We achieve this by multiplying the primes to determine a unique number for a sequence of any length, since each dancer has unique label each product will be unique. Hence, any numeral names a unique object, whether it be a sequence of dancers or a lonely dancer. So we can see that

#< a_{1}, b_{2} > = 2^{a_{1}+1} \cdot 3^{b_{2}+1} = 2^{2+1} \cdot 3^{3+1} = 2^{3} \cdot 3^{4} = 8 \cdot 81 = 648.

More succinctly, we could say:

#<a_{1}* b_{2} > = 648.

We need to do a little more work to show that this labeling system will allow us to recover the structure of each congo line by decoding. But of course all we need to do here is perform a prime factorisation, from which it is straightforward to recover that 648 = 2^{3} \cdot 3^{4}, from which we can unpack by definition our initial sequence as desired. This same pattern holds for more complicated congo lines.

Talking about dancing

We can now define several functions which will help us talk about dancing. Firstly we describe our congo line as a sequence, as only lines with this property are encoded by the prime-coding technique we used above. The following definitions apply to sequence numbers only. But they’re pretty straightforward. You might want to describe the length of a congo line, or recover the participants from the #name we have given the line, and we can do this with the following function. Let a := <a_{1}*a_{2} .... *a_{n} >, and define

  1. Seq(a) := \forall p, q \leq a (Prime(p) \wedge Prime(q) \wedge q< p \wedge p | a \rightarrow q|a) \wedge a \neq 0. [Sequence Number]
  2. lth(a) := \mu k \leq a+1 ( \neg (p_{k} | a)) [Length]
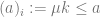
  3. (a)_{i} := \mu k \leq a ( (p_{i}^{k} | a \wedge \neg (p_{i}^{k+1} | a) \dot{-}1). [Decoding]

So let’s see how the length of a string can be recovered. From any number #(a) we have its prime factorisation, so the trick to decomposing each element in the factorisation, for instance take lth(12) and we find that  p_{3} = 5 \wedge \neg(5 | 12) and then we see that lth(12) = lth(<2^{2} \cdot 3>) = 3. In general lth(a) = n+1 where a = <a_{1} .... a_{n}> because <> = 1 by definition.

Similarly, we check (12)_{1} by finding that p_{1} = 2, and p_{1}^{2} = 4 which divides 12 but we also have p_{1}^{3} = 8 does not divide 12 as desired. So we have k = 2 which is positive as desired. Next we test (12)_{2} by observing p_{2} = 3 and choosing p_{2}^{1} = 3 so choose k = 1, so that we have 3 divides 12, but 9 does not. Furthermore 3 is positive, so we can conclude that the 12 decodes into its unique prime factorisation 2^{2} \cdot 3. Here we knew in advance the correct decoding, but in general we test the appropriateness of a decoding procedure by multiplying each sequentially discovered component until such time as the product reaches (or exceeds) the coded number, (12) in our case.

Talking about anything else.

So far we have suggested that we could use this coding technique to simplify discussions about congo lines, but this is merely one application. In fact the prime-coding technique is versatile enough to encode any structure. In particular we shall come to see how it can effectively encode sentences of the rich logical language \mathbb{L} and the sequential action of Turing machines. The same fundamental idea underlies both approaches, we wish to be able to take any string of sentences < \phi_{1}, .... \phi_{n} >, or action sequence < a_{1}, .... a_{n} > and code them in the natural numbers, so that we may give each sequence a name. We adopt the following notation:

\ulcorner n_{i} \urcorner \text{ is the godel number of } \phi_{i}

This utility allows us to express claims about the object \ulcorner n_{i} \urcorner in our language \mathbb{L}. So if \mathbb{L} is a rich first order language capable of speaking about numbers, we can treat \ulcorner n_{i} \urcorner as first order object and make expressive claims about the properties of the object in question. This is a key point, your language must be sufficiently expressive to talk about numbers in the first place, if we are going to use numbers as a code for other objects! In our case the object is the sentence \phi_{i}, so defining a predicate: N(x) := \{ x | x \text{ are nice sentences } \} we can claim N(\ulcorner n_{i} \urcorner ) and expect to be able to evaluate such a claim according to the semantics of \mathbb{L}.

The generality of this technique is truly staggering once you perceive it. Any language, or system capable of identifying  the natural numbers can use the prime coding technique to code its own expressions is then capable of expressing claims about its own syntax. Allowing the expression of a “meta-level” reflection about the properties of any constructions developed within our own language. Constructions such as novels, poems and proofs – some of which are certainly nice.

This expressivity allows for Godel’s famous incompleteness result; about which, more later.